Isolant

Après vous avoir montrés différent isolants, ayant chacun leurs propriétés et leurs dérivés, la question serai de savoir comment fonctionnent ces isolants thermiques.

« Quelle est la science derrière les diffèrent isolants écologiques et qu’est-ce que l’énergie grise ? »

Allons voir plus en détail la propriété des matériaux.

Abordons le sujet en commençant au niveau moléculaire :

Nous allons aborder une transmission de chaleur qui se produit entre deux milieux différents séparés par un intermédiaire (ici, l’isolant).

La conduction (disponible Partie II, Thermique) :

La conduction thermique (ou diffusion thermique) est un mode de transfert thermique provoqué par une différence de température entre deux régions d'un même milieu, ou entre deux milieux en contact, et se réalisant sans déplacement global de matière (à l'échelle macroscopique). Elle peut s'interpréter comme la transmission de proche en proche de l'agitation thermique : un atome (ou une molécule) cède une partie de son énergie cinétique à l'atome voisin.

La conduction thermique est un phénomène de transport de l'énergie interne dû à une hétérogénéité de l'agitation moléculaire. C'est donc un phénomène irréversible. Dans les fluides (liquides et gaz) ce transport d'énergie résulte de la non uniformité du nombre de chocs par unité de volume, de façon analogue au phénomène de diffusion. Dans les solides, la conduction thermique est assurée conjointement par les électrons de conduction et les vibrations du réseau cristallin (phonons)

Dans une maison, il y a transmission de chaleur dans celle-ci. Par exemple, lorsque nous allumons le chauffage ou lorsque nous avons une toute autre source de chaleur (Au lieu de rayonnement), les molécules d’air se transmettent l’énergie thermique entre-elles.

Ensuite, les molécules essayent de transmettre leur chaleur d’un Milieu A à un Milieu B. Ceci fait qu’il y a une grande perte de chaleur.

On installe donc des isolants. C’est isolants sont composés d’air qui ne peuvent bouger et qui ne sont pas en contact ni avec le Milieu A ou B et donc la transmission thermique est faite plus lentement et ainsi la chaleur reste dans le Milieu A.

Grâce à cette propriété, la transmission de chaleur et considérablement ralentit et donc moins de perte de chaleur à l’intérieur de la maison.

Nous pouvons aussi directement utiliser cette propriété sur les fondations même de la structure comme ci-dessous.

Après avoir vue les propriétés des isolant au niveau moléculaire, penchons-nous au niveau physique, une calcul permettant de connaître la résistance thermique R d’un matériau :

Cette résistance R s’applique aux solides ainsi qu’aux fluides (liquide ou gaz) sur une surface.

Dans le Système international des unités, elle est donnée en Mètre Carré-Kelvin par Watt (m2·K·W) pour la Resistance Thermique d’une Surface.
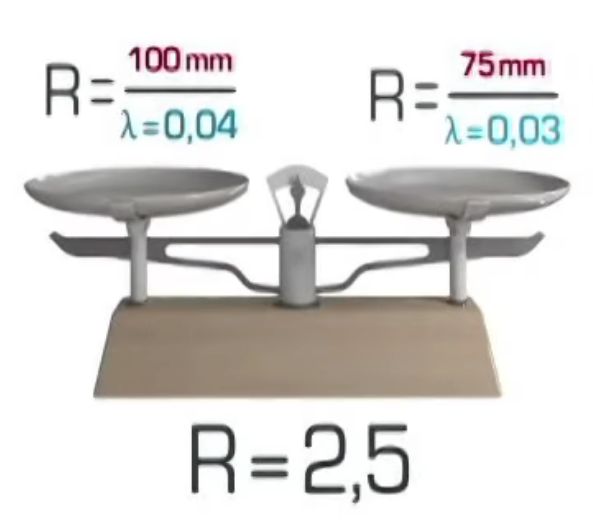
R dépend de l’épaisseur de E et du Coefficient Lambda λ.

R (Resistance Thermique) :

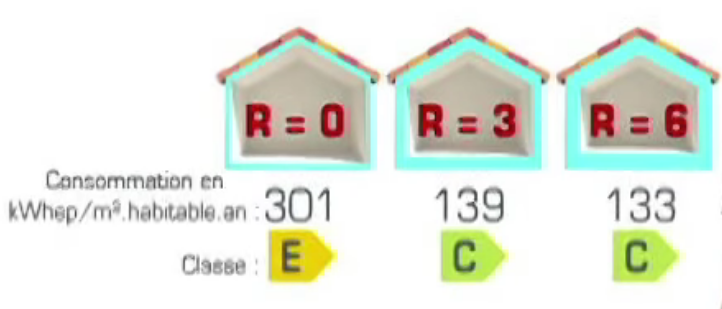
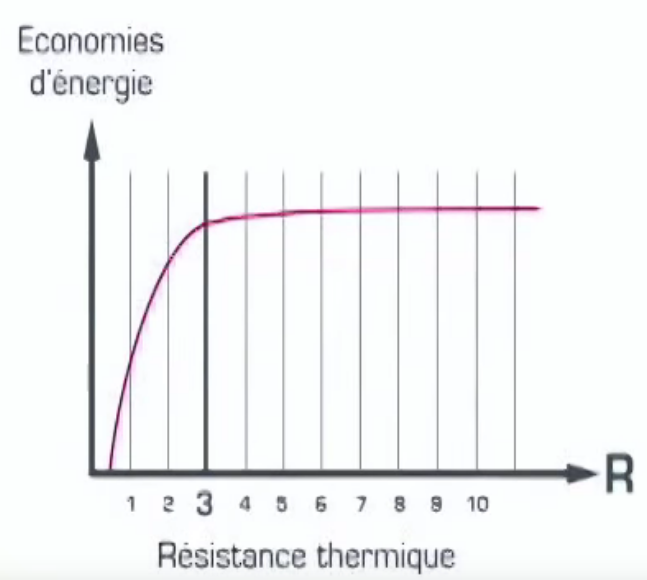
La résistance thermique R indique la tendance d’un élément de construction à résister au passage de la chaleur.
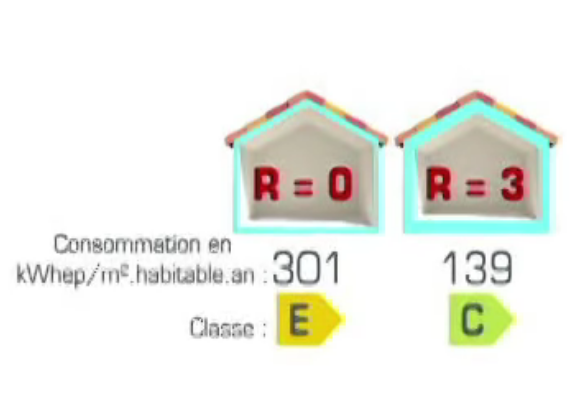
La valeur R donne une information sur la performance d’isolation d’un élément de construction (mur, toit, plancher, porte, fenêtre...). Elle indique la quantité de chaleur qui passe en une seconde à travers une surface de 1 m2. L’unité de la Valeur R s'exprime en Mètre Carré-Kelvin par Watts (m2·K/W).
Plus R est important, plus l’élément est isolant.

λ lambda (Coefficient de Conductivité Thermique) :

Le Lambda λ ou conductivité thermique d’un matériau, représente la capacité d’un matériau à conduire la chaleur. λ (lambda) d’un matériau représente le flux de chaleur qui passe en une seconde à travers une surface de 1 m2 et une épaisseur de 1 m (autrement dit à travers un cube d’un mètre de côté), lorsqu’il y a une différence de température de 1°C (équivalent à un degré Kelvin).
λ est une caractéristique d'un isolant. Il sert à déterminer la résistance thermique (R) d’une épaisseur donnée (E).
Plus la valeur λ d’un isolant est faible plus la conductivité thermique entre l’intérieur et l’extérieur augmente. Valeur λ s'exprime en Watts par Mètre par Kelvin (W/m/K).
Plus lambda est petit, moins le matériau laisse perdre de chaleur pour une même épaisseur.
Le béton, l’acier, la brique, le bois ou les matériaux isolants ont des conductibilités thermiques très différentes : l’aluminium est, par exemple, 5000 fois plus conducteur que la laine de verre.

e (Epaisseur de l’isolant) :

« e » est l’épaisseur de l’isolant et s’exprime en mètre (m).

Rappel des Unités :

Valeur R s'exprime en Mètre Carré-Kelvin par Watts (m2·K/W).
Valeur λ s'exprime en Watts par Mètre par Kelvin (W/m/K).
Valeur e s’exprime en mètre (m).

Par exemple, nous pouvons obtenir deux valeurs R identiques pour des valeurs e et λ différentes entre-elles.

Ici pour R = 2.5 on peut soit avoir :
1)Une épaisseur « e » = 100mm / 0.1m pour un Lambda λ = 0.04
2)Une épaisseur « e » = 75mm / 0.075m pour un Lambda λ = 0.03

Consommation selon l’isolant :

La consommation de la maison varie selon la résistance thermique R.
La chaleur est donc plus ou moins gardée au sein de la maison et donc la consommation et les dépenses baisses.

Ici, La maison :
1) Classé E ayant R = 0 utilise 301 kWhep/m2.habt.an*
2) Classé C ayant R = 3 utilise 139 kWhep/m2.habt.an*
*kWhep/m2.habt.an : kilo Watts-heures d’énergie primaire par mètre carré habitable par ans.
La maison classé E dépense plus que celle classé C.

Ici « l’étiquette énergétique » ou « diagnostic de performance énergétique » (DPE).

Toutefois, le fait d’avoir un R > 3 / 7 ne signifie pas que la consommation baisse de manière visible.

Ici, la consommation passe d’une baisse de 54% entre la 1ère maison et la 2ème maison à une baisse de 56% entre la 1ère maison et la 3ème maison.

Sur cette courbe « la méthode d’évaluation du DPE », et nous pouvons voir que la courbe stagne à un R = 3.

Pour finir, nous terminerons par l’énergie grise.

En théorie, un bilan d'énergie grise additionne l'énergie dépensée lors de :

la conception du produit ou du service ;

l'exploitation de la ressource ou de la matière première ;

l'extraction et du transport des matières premières ;

la transformation des matières premières et la fabrication du produit ou du service ;

la commercialisation ;

l'entretien, des réparations, des démontages du produit dans son cycle de vie ;

du recyclage du produit en fin de vie.

L'énergie incorporée désigne généralement l'énergie nécessaire à la fabrication du matériau (mais non à sa mise en œuvre ou fin de vie).

Le fait d’isoler sa maison et respecter l’environnement n’est toujours pas compatible.
Il faut donc bien sûr prendre en compte ce détail.

Exemple :

Un Watt équivaut à un Joule par seconde

Bottes de paille : 0,001 MWh/m3 ;
Matériau bois : 0,1 à 0,6 MWh/m3 ;
Béton cellulaire : 0,54 MWh/m3 ;
Bloc de béton : 0,7 MWh/m3 ;
Polystyrène expansé : 0,3 à 0,85 MWh/m3 ;
Brique pleine : 1,2 MWh/m3 ;
Béton armé : 1,85 MWh/m3 ;
Acier recyclé : 24 MWh/m3 ;
Acier primaire : 52 MWh/m3 ;
Cuivre : 140 MWh/m3 ;
Zinc – titane : 180 MWh/m3 ;
Aluminium : 190 MWh/m3.

MWh/m3 : MegaWattHeure par Mètre Cube (3)

Le mégawatt (MW), soit un million de watts (106 W), est une unité fréquemment utilisée en production électrique ; un réacteur nucléaire français a une puissance installée comprise entre 900 MW et 1 450 MW électriques.

Afficher la suite de cette page